数学Ⅲ ~無限等比数列が収束する条件~
公開日:
:
最終更新日:2021/06/16
数学Ⅲ
数学Ⅲ、無限等比数列が収束する条件の例題と問題です。
無限等比数列が収束する条件は、公比rがー1<r≦1のときです。
-1<r<1とする人が相当多いので気を付けましょう!
迷った場合は、7つ場合分けして確かめておきましょうね。
あと、分母がプラスかマイナスかわからない場合は、解説動画のように場合分けするか、分母の値を2乗して(2乗するとプラスだから)不等式全体に掛けると解くことができます。

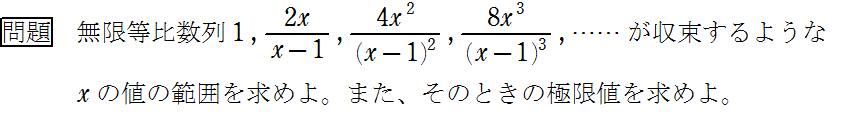
解説動画
スポンサードリンク
関連記事
-

-
数学Ⅲ 複素数平面 ~三角形の形状①~
数学Ⅲ、複素数平面の三角形の形状①の例題と問題です。 角の大きさと同じで、γ-α/β-αを求
-

-
数学Ⅲ 複素数平面 ~n乗根の計算(ド・モアブルの定理)~
数学Ⅲ、複素数平面のn乗根の計算の例題と問題です。 ド・モアブルの定理として有名ですね。
-

-
数学Ⅲ 複素数平面 ~方程式の表す図形①~
数学Ⅲ、複素数平面の方程式の表す図形①の例題と問題です。 基本は、絶対値2つで垂直二等分線、
-

-
数学Ⅲ ~数列の極限① 一番大きな次数で割るorくくるタイプ~
数学Ⅲの数列の極限に関する例題と問題です。 数列の極限は、 ① 一番大きな次数で割るor
-

-
数学Ⅲ 複素数平面 ~複素数の乗法・除法~
数学Ⅲ、複素数平面の複素数の乗法・除法の例題と問題です。 絶対値を2つにわけれるので、それを
-

-
数学Ⅲ ~数列の極限② 分母・分子の有理化~
数学Ⅲの数列の極限に関する例題と問題です。 数列の極限は、 ① 一番大きな次数で割るor
-

-
高校数学 問題検索 数学Ⅲ 微分 「商の微分法」
㊟問題文をクリックしてください! 解説動画のリンクが別枠で開きます(`・ω・´) &nb
-

-
数学Ⅲ ~漸化式の極限①~
数学Ⅲ、漸化式の極限の例題と問題です。 今回は、特性方程式型の漸化式の極限を調べます。
-

-
高校数学 問題検索 数学Ⅲ 微分 「合成関数の微分法」
㊟問題文をクリックしてください! 解説動画のリンクが別枠で開きます(`・ω・´) &nb
-

-
数学Ⅲ ~場合分けによる極限~
数学Ⅲの場合分けによる極限の例題と問題です。 無限等比数列において、公比が文字rで表されている
- PREV
- 数学Ⅲ ~和で表された数列の極限~
- NEXT
- 数学Ⅲ ~漸化式の極限② 分数型漸化式~

