数学Ⅲ ～無限等比数列が収束する条件～
公開日：
:
最終更新日：2021/06/16
数学Ⅲ
数学Ⅲ、無限等比数列が収束する条件の例題と問題です。
無限等比数列が収束する条件は、公比ｒがー1＜ｒ≦１のときです。
－1＜ｒ＜１とする人が相当多いので気を付けましょう！
迷った場合は、７つ場合分けして確かめておきましょうね。
あと、分母がプラスかマイナスかわからない場合は、解説動画のように場合分けするか、分母の値を2乗して(2乗するとプラスだから)不等式全体に掛けると解くことができます。
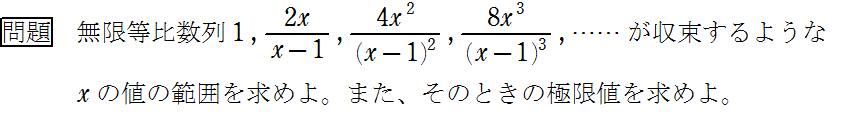
解説動画
スポンサードリンク
関連記事
-
-
数学Ⅲ 複素数平面 ～ｗ＝１/ｚが描く図形～
数学Ⅲ、ｗ＝z分の1が描く図形の例題と問題です。 図をかき、式で表して、変形、代入という順番
-
-
数学Ⅲ 複素数平面 ～複素数の絶対値～
数学Ⅲ、複素数平面の複素数の絶対値の例題と問題です。 今回も2乗の公式が出てきます。必ず両方
-
-
数学Ⅲ 複素数平面 ～複素数の点の移動① 回転～
数学Ⅲ、複素数平面の複素数の点の移動の例題と問題です。 今回は回転です。 複素数平面の
-
-
高校数学 問題検索 数学Ⅲ 微分 「陰関数（円・楕円・双曲線）の微分」
㊟問題文をクリックしてください！ 解説動画のリンクが別枠で開きます(｀・ω・´) &nb
-
-
数学Ⅲ ～数列の極限③ 一番大きな数で割るorくくるタイプ～
数学Ⅲの数列の極限に関する例題と問題です。 数列の極限は、 ① 一番大きな次数で割るor
-
-
数学Ⅲ ～場合分けによる極限～
数学Ⅲの場合分けによる極限の例題と問題です。 無限等比数列において、公比が文字ｒで表されている
-
-
高校数学 解説動画 数学Ⅲ 微分 合成関数の微分法
さて今回は、微分の中でも最重要と言える、合成関数の微分です。 この後に続く、三角関数、指数関数
-
-
数学Ⅲ ～和で表された数列の極限～
数学Ⅲ、和で表された数列の極限の例題と問題です。 基本的にΣ(シグマ)記号を扱っていきます。
-
-
高校数学 解説動画 数学Ⅲ 微分 積の微分法
さあどんどん微分していきましょう(｀・ω・´) 次は積の微分法です。
-
-
数学Ⅲ 微分・積分 公式集
数学Ⅲの微分・積分では、いくつかの必須公式があります。 公式を０から作って
- PREV
- 数学Ⅲ ～和で表された数列の極限～
- NEXT
- 数学Ⅲ ～漸化式の極限② 分数型漸化式～
